Nota: Se procura uma pseudoforça ou força inercial, veja Força inercial centrífuga.
As chamadas centrífugas são aparelhos construídos a fim de permitirem a separação de substâncias que possuam densidades diferentes em uma mistura via decantação. É utilizada, a exemplo, na separação dos elementos sanguíneos.
Tipos de centrífugas
Existem diferentes tipos de centrífugas, sendo algumas para propósitos muito específicos, como as de separação de isótopos. As centrífugas variam em tamanho e velocidade, e o uso de cada uma depende da quantidade e dos tipos de substâncias a serem separadas. Podem ser divididas em centrífugas industriais e laboratoriais.
Basicamente, as centrífugas contêm dois componentes essenciais:
- Fixo. Os tubos que ficam em um ângulo fixo em relação ao eixo de rotação. Eles são usados para grandes volumes.
- Inclinado. Os tubos são pendurados no interior das caixas ligado ao veio do rotor. Eles giram quando o movimento rotativo. Eles são usados para pequenos volumes e para a separação de partículas do coeficiente de sedimentação igual ou quase igual. O mecanismo de rotação é colocado dentro de um recipiente, de cerca de 4 ° C. Se a câmara para rodar devido ao atrito com o ar, a temperatura da amostra pode ser aumentada desnaturado.
Numa centrifugadora, as massas das amostras devem ser compensadas uns as outras. Caso contrário, podem "explodir". Para que isso não aconteça quase todas estas máquinas param se as massas não são compensadas.
Centrifugadora de papel
A centrífuga é uma ferramenta essencial para hospitais e laboratórios em todo o mundo. O problema é que as centrífugas são caras, volumosas e requerem eletricidade. Em regiões pobres onde as doenças tropicais florescem, esses instrumentos podem ser difíceis de obter, limitando assim a capacidade dos trabalhadores de saúde do ponto de atendimento de fazer seu trabalho. A centrifugadora de papel, de baixo custo (menos de um real), leve (2 g) e alimentada por energia humana foi concebida com base num modelo teórico inspirado na mecânica fundamental de um antigo brinquedo, "Zunca-zunca". Em 2017, dois pesquisadores da Stanford criaram a centrífuga de papel que pode revolucionar como infecções como malária e HIV são detectadas nos países em desenvolvimento.
História
Em meados do século XVIII a Inglaterra, recém-industrializada, importava grandes quantidades de queijo e leite. Os fazendeiros americanos, em face da oportunidade, foram em busca de meios de aumentar a sua produção de modo a atender a esse mercado. O processo usado até então para desnatar leite, baseado na decantação, era lento e obsoleto, pois o leite fresco era deixado em repouso, por até 24 h, até que a nata depositasse na superfície para depois ser retirada.
Em 1864, o alemão Antonin Prandtl (1842-1909), desenvolveu o primeiro separador mecânico que usava a força centrífuga. Era um equipamento rústico no qual baldes eram presos a hastes conectadas a um rotor de operação manual. Após um tempo o leite desnatado se depositava no fundo do balde e a nata estava na superfície. A maquina era então parada e a nata removida.
Em 1879, Karl Gustaf Patrik de Laval (1845-1913), engenheiro mecânico sueco, patenteou um sistema funcional para essa separação que operasse de forma continua, no qual o separador poderia ser esvaziado e limpo durante a operação Tratava-se de um sistema precursor do sistema de centrifugação do tipo cesta. Dez anos depois, o alemão Clemens von Becholsheim (1852-1930) introduziu melhorias para o separador de Laval, os chamadas "pratos alfa". Esse sistema dividia o leite em finas camadas, o que aumentava a eficiência da separação
Desde o final do século XIX, quando da fabricação dos primeiros modelos, os fabricantes promoveram diversas melhorias nas centrífugas. Essas melhorias abrangem os materiais utilizados na fabricação, o sistema de engrenagem, o aumento da segurança operacional, a aparência e os materiais utilizados no acabamento
Princípio de funcionamento
O princípio de funcionamento das centrífugas baseia-se na forma com a qual a força centrípeta necessária depende de grandezas como a massa, a velocidade tangencial, a velocidade angular e o raio da trajetória associados à partícula no movimento circular em consideração:
Nesta expressão m corresponde à massa do objeto, v à velocidade tangencial de tal objeto, r ao raio da trajetória e refere-se à velocidade angular do objeto em consideração.
Nas centrífugas, encontrando-se os componentes da mistura todos confinados ao recipiente, é notória a condição de que todos deverão, no equilíbrio dinâmico à velocidade máxima, descrever movimentos circulares dotados de mesma velocidade angular . Todos completam uma volta, descrevendo por tal um arco de 360º = radianos, em um mesmo intervalo de tempo - em um mesmo período T.
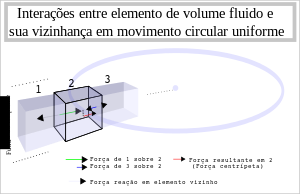
Em rais condições, a força centrípeta requerida em um dado elemento de volume no meio do fluido deve ser provida pela resultante de forças normais oriundas da interação deste elemento com sua vizinhança. Tal resultante de forças depende em sentido radial da interação deste elemento de volume com o elemento que descreve uma trajetória de raio maior que o raio de sua própria trajetória, elemento último que lhe serve de apoio, e com o elemento de volume em lado oposto, que descreve trajetória com raio ligeiramente menor e para o qual o elemento de volume em questão fornece apoio. Devendo a força resultante destas duas interações - a força centrípeta no elemento central - apontar na direção do elemento vizinho cuja trajetória tem menor raio, ou seja, para o centro da curva, é notório que a interação entre o elemento central e o elemento vizinho mais ao centro deve ser menor do que a interação entre o elemento central e o seu vizinho em trajetória de maior raio. Elementos de volume mais internos têm à sua disposição forças de apoio e por tal também forças centrípetas disponíveis máximas menores do que as forças de apoio disponibilizadas aos seus conterrâneos que encontrem-se em trajetórias de maior raio, o que traduz-se fisicamente pela afirmação de que as pressões em pontos no interior do fluido mais próximos ao fundo do recipiente são maiores do que as pressões em pontos no interior do líquido juntos à superfície deste. Seguindo-se a mesma linha de raciocínio verifica-se que tanto maior será esta diferença de pressão quanto maior for a força centrípeta necessária a cada elemento de volume em consideração. Em linguagem mais específica, visto que para um mesmo raio a força centrípeta aumenta em proporção quadrática com a velocidade angular, consideravelmente maior será o gradiente de pressão quanto maior for a velocidade angular da centrífuga em questão. Como a força centrípeta necessária também depende da massa encerrada no elemento de volume - aumentando de forma diretamente proporcional a esta - tanto maior será o gradiente de pressão quanto maior for a densidade do elemento de volume em consideração.
A maior das forças de interação entre um elemento e sua vizinhança ocorre pois no elemento diretamente em contato com o vidro no fundo do recipiente, e a força que este aplica ao elemento situado em vizinhança radialmente oposta deve ser menor do que o apoio que este recebe do vidro por uma parcela igual à força centrípeta necessária ao seu próprio movimento circular. Tal raciocínio estende-se de forma apropriada a todos os elementos de volume radialmente alinhados de forma que a pressão é tanto maior quanto maior a profundidade no fluido. Matematicamente o raciocínio apresentado pode ser resumido via expressão:
onde representa a densidade do elemento de volume , "a" representa a aceleração requisitada à manutenção de sua posição radial - a aceleração centrípeta no caso - e "dr" representa a espessura radial deste elemento de volume. Esta expressão é em muito similar equação fundamental da hidrostática estabelecida mas análise de variações de pressão com a profundidade em fluidos sob a ação da gravidade, expressão cujo mecanismo de dedução mostra-se em muito parecido ao apresentado. A análise dos elementos de volume à situação gravitacional fornece por resultado:
onde g é a aceleração da gravidade e dh o diferencial na altura, ou seja, a altura do elemento de volume "dv" em consideração medida de forma paralela à direção estabelecida pela gravidade. A situação é simplificada no caso hidráulico dado que a densidade da água pode ser considerada praticamente constante durante uma ampla faixa de pressões, o que nos leva à expressão para fluidos homogêneos incompressíveis:
muito comum nos cursos de hidrostática em nível secundário.
Contudo, para a análise de fluidos compressíveis como o ar atmosférico ou de misturas fluidas de substâncias heterogêneas "incompressíveis" contudo com densidades distintas - caso último o caso geral aqui em interesse - a integral não se mostra tão simples visto que a própria densidade a considerar-se dependerá da profundidade no fluido, sendo esta distribuição de densidade no equilíbrio o ponto de interesse no problema aqui em consideração.
Retomados a situação inicialmente exposta bem como o referencial inercial adequado, caso haja um elemento de volume em menor raio a encontrar-se em situação tal que a força centrípeta necessária ao seu movimento em tal raio faça-se maior do que o valor de apoio máximo encontrável em seu vizinho de maior raio - o que ocorre caso a massa deste elemento de volume seja consideravelmente maior do que a daquele a servir-lhe de apoio - visto que a força centrípeta necessária cresce com a massa e por tal com a densidade do elemento de volume - é notório que este elemento mais interno não encontrar-se-á solicitado pela força centrípeta necessária ao seu movimento. "Saindo pela tangente" dado tratar-se de uma solução fluida, este elemento desloca o elemento vizinho incapaz de prover-lhe apoio e toma-lhe o lugar a fim de encontrar um elemento que lhe forneça o apoio e a força centrípeta necessária ao seu movimento. Ao fazê-lo, este elemento - cuja massa não se altera - passa a mover-se em trajetória com maior raio - deslocando-se em direção ao fundo do recipiente - o que, mantida a velocidade angular e visto que à velocidade angular e massas constantes a força centrípeta requisitada cresce com o raio, implica agora maior força centrípeta necessária a seu movimento. A situação se repete novamente, contudo de forma mais acirrada, com o novo vizinho, até um estado de equilíbrio possa por este elemento ser alcançada. Dado tal raciocínio compreende-se porque o recipiente contendo os componentes a serem separados são inseridos nos extremos do mecanismo de giro nas centrífugas.
Possuindo menor massa dada sua menor densidade, contudo, o elemento antes em raio mais externo - uma vez expulso para as regiões mais próximos à superfície do fluido - pode agora manter-se em trajetória adequada à sua posição mediante a força de apoio menor que seu vizinho - agora o mais denso - é capaz de aplicar-lhe visto ser a força centrípeta requisitada a este elemento de volume também menor. A força necessária ao seu movimento faz-se consideravelmente menor dadas tanto à diminuição do raio como da massa encerrada no elemento de volume. Como consequência, uma situação de equilíbrio será atingida com os elementos dispostos radialmente em função de suas respectivas densidades, encontrando-se os elementos menos densos na superfície do fluido - descrevendo trajetórias com raios menores - e os elementos mais densos no fundo do recipiente, descrevendo trajetórias com raios maiores.
Ocorre assim a separação dos componentes na mistura inicial, objetivo final na construção de uma centrífuga. Tem-se uma distribuição de densidades tal que os componentes mais densos servem de "apoio" para os componentes menos densos.
Referencial não-inercial
Tratando-se da separação de partículas sólidas dispersas em solução liquida, ou de demais dispersões de partículas em fluidos - mantidas as densidades fixas - a explicação da separação em função das densidades nas centrífugas mostra-se muito parecida à explicação apresentada para explicar-se a flutuabilidade de objetos em fluidos desde que assumido um referencial não-inercial girante onde o recipiente e seu conteúdo em centrifugação permaneçam sempre estáticos. Aparte consideração à frente, a analogia é direta, bastando para tal considerar que a aceleração no caso hidrostático típico é devida à gravidade ao passo que no caso da centrífuga e no referencial adotado, a força centrífuga percebida neste referencial faz o papel da força da gravidade encontrada no primeiro caso. Verifica-se assim que os objetos menos densos inicialmente imersos nos fluidos mais densos flutuam neste devido ao "empuxo" que sobre eles atua, força esta maior que o peso deste objeto no caso gravitacional e maior do que a força centrífuga a ele associada no segundo caso. Quando o objeto possui contudo densidade maior do que a do fluido verifica-se pois que o "empuxo" resultante é menor do que o peso no caso hidrostático e menor do que a "força centrífuga" no caso da centrifugação: objetos mais densos que o fluido afundam em seus respectivos fluidos. Pode-se assim em princípio separar a mistura em questão valendo-se apenas da gravidade, contudo a centrífuga traz a vantagem de que as acelerações centrípetas - no referencial não-inercial adotado traduzidas por "forças centrífugas" - podem ser feitas ordens de grandeza maiores do que a aceleração da gravidade, o que agiliza em ordens de grandeza a separação desejada. A analogia só não é de todo precisa porque a força centrípeta na partícula e por tal a "força centrífuga" que nela atua no referencial não inercial são dependentes do raio da trajetória, aumentando com este à velocidade angular constante, ao passo que a gravidade é para todos os efeitos constante ao longo da extensão dos recipientes normalmente considerados.